Shortie (SBJ) is a blackjack side bet that is an extreme version of the “Under 13” bet (see this post). Quite simply, SBJ wins if the player’s first two cards total 9 or less (where Aces always count as 1). Note that if the player is dealt a Nine or a ten-valued card, then obviously his SBJ wager immediately loses. For this reason, it should come as little surprise that SBJ is highly countable.
The game developer for SBJ hired a well-known expert to conduct a card counting analysis. I am overjoyed that developers are now considering such an analysis to be an essential component of bringing a new game to market. On the other hand, I have a problem with this particular analysis. While it was performed by one of the best in the industry, our results do not agree. The other mathematician arrived at a substantially lower win-rate than I am going to present here. I asked the other mathematician to double-check his work. He did not report back.
I was able to get independent confirmation of my results from Charles Mousseau of Total Gaming Science. As you will see below, I came up with a win-rate of 3.59 units per 100 hands based on a simulation of 1B shoes. Charles arrived at a win-rate of 3.62 units per 100 hands based on a simulation of 1M shoes. My personal thanks to Charles for his help confirming these results.
SBJ has been around for a few years in a slightly different format, where the player could place his winnings from SBJ (if any) on his main blackjack bet, much like “War Blackjack.” The ability for the player to parlay his winnings formed the core element of how the wager was marketed to casinos. Indeed, SBJ gained a certain amount of infamy for its logo, which is one of my all-time favorites:

The version I will analyze here is a straight-up blackjack side bet based on the player’s first two cards, In the case when the player is dealt a pair of Aces, the dealer’s up-card is also considered. There is no parlaying of winnings.
Here is the most common pay table:
- A-A-A suited pays 800-to-1.
- A-A-A unsuited pays 100-to-1
- A-A (dealer does not have Ace) pays 25-to-1
- 2-2, 3-3, 4-4 pays 6-to-1
- Total points = 3, 4, 5, 6 pays 3-to-1
- Total points = 7, 8, 9 pays 2-to-1
The following table gives the combinatorial analysis in the six-deck case:
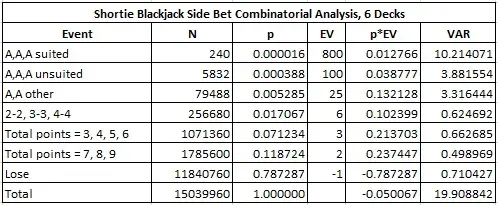
In particular,
- The house edge is 5.0067%
- The standard deviation is 4.4619
- The hit frequency is 21.2713%
The following table gives the effect of removals in the six-deck version, together with a balanced card counting system based on the EORs:

Note that removing a single Ace from a six-deck shoe moves the house edge 2.382% towards the house, while removing a 9 or T moves the house edge towards the player by 0.626%. These are very large values for the EORs, considering that these changes result from removing only one card out of 312.
As indicated in this table, the balanced card counting system I will consider is:
- System: (-4, -1, -1, -1, 0, 0, 1, 1, 1, 1).
This is a very accurate card counting system, with betting correlation 0.9899.
The following table gives the results of card counting SBJ in a six-deck shoe, using the system given above. These results were obtained by a simulation of one billion (1,000,000,000) six-deck shoes with the cut card placed at 260 cards (one deck from the end):
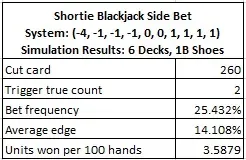
A win rate of 3.59 units per 100 hands makes SBJ a very strong opportunity for the AP. Few side bets rival this win-rate and those that do are among the most vulnerable presented in this blog. Among the side bets I’ve analyzed, only Slingo (see this post) and Super Sevens (see this post) have higher win-rates, and both of these wagers are extinct. SBJ has a higher win-rate than Red Flex, which the developer now recommends dealing only from a continuous shuffle machine.
Another way to measure the vulnerability of SBJ to card counting is by considering its desirability index (DI) (see this post). With a DI of 15.92, SBJ has risk comparable to Field Gold 21, Over/Under 13, Red Flex and Slingo, all of which are ranked “high” or “extreme.”
The reason all of this makes me nervous is that the other mathematician came up with a win-rate of 0.792 units per 100 hands (using a slightly weaker unbalanced counting system). That is about 22% of the win-rate I achieved. He states that SBJ is “moderately vulnerable to card counting.” I disagree with his assessment, but then again ...


