The Dragon Bonus baccarat side bet (DB) is the most popular proprietary side bet for baccarat on the market. Only the "Pair" side bet is more common, perhaps because it is in the public domain. I describe card counting DB in this post. My conclusion was that DB has at most a minimal vulnerability to card counting. With the cut card placed at 14 cards and the normal burn-card rule at the start of the shoe, the AP can win about 0.1231 units per shoe, or about 0.1515 units per 100 hands. In this post I am going to consider shoe-shopping DB.
Shoe-shopping is possible in casinos that have a lot of tables of baccarat, as is common in many casinos throughout Asia. We assume that an AP is wandering the casino floor watching for new shoes. When the AP finds a new shoe, he waits to see the number of burn cards for that shoe. Using the standard burn-card rule, the number of cards that are dealt face down is equal to the number of pips on the first card out of the shoe. If the first card is a face card, then 10 cards are burned. The AP is looking for a good shoe, which means as few burn cards as possible. In the best possible case, when an Ace is the first card, only one card is burned. The AP can do no better than this.
In considering the possible gain for an AP who is shoe-shopping, we can analyze each possible number of burn cards (1 to 10) and give statistics for each number of burn cards. We can do this comparison for various cut-card placements, perhaps from the standard placement of 14 cards up to the very safe 104 cards (2 decks). Essentially we can generate a lot of data. I am going to forgo a full analysis and get to the point. I am going to only consider the best possible first card (an Ace), with the understanding that this gives an absolute upper bound on the gain possible from shoe-shopping.
There are a couple of arguments here that I don't want to have. The first is that it takes time to wander the floor and find good shoes. This may consume more of the AP's time than the value of playing each shoe to its end. I am going to use the "Jack Rabbit" assumption: the AP who finishes one shoe immediately finds another shoe that has an Ace as its first card. It is clear that this is the best the AP can do.
The other argument is that the AP can "Wong out" of bad shoes. In other words, if the count on a shoe becomes sufficiently bad, then the AP should leave the shoe and look for another one. The AP should not waste time chasing bad shoes to their end. This method is commonly used for blackjack and certainly applies here. In blackjack, the "Wong out" point is typically a true count of -1, more or less, with the Jack Rabbit assumption. At some point I may analyze the AP who both shoe-shops and Wongs baccarat side bets, using the Jack Rabbit assumption. That's for another day.
Back to the matter at hand. First a review of the Dragon Bonus wager and its combinatorial analysis.
To play DB, a wager is made on the side bet on either the player or banker side. The DB wager wins if the side wagered on wins by a natural, or else wins by 4 or more points. The most commonly used pay table is the following:
- Natural win (two card 8 or 9) pays 1-to-1.
- Natural tie (two card 8/8 or 9/9) is a push.
- Win by 9 pays 30-to-1.
- Win by 8 pays 10-to-1.
- Win by 7 pays 6-to-1.
- Win by 6 pays 4-to-1.
- Win by 5 pays 2-to-1.
- Win by 4 pays 1-to-1.
- All other results lose.
The table below gives the combinatorial analysis for this wager. In particular note that the house edge for the player side of the DB wager is 2.652%, but the house edge for the banker side of the DB wager is a much larger 9.373%.
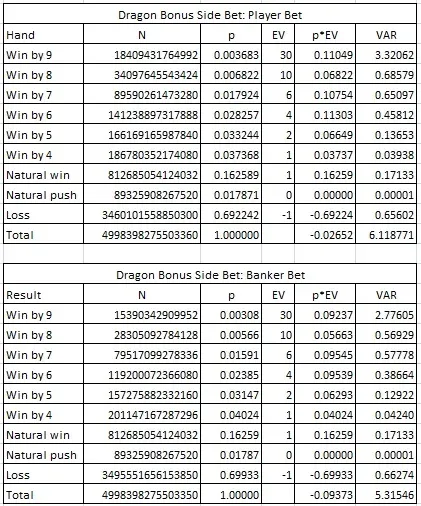
By considering the house edge of each side (player = 2.652%, banker = 9.373%), the only reasonable approach for the card counting AP is to target the player side of the DB bet. In this blog post, I showed that the AP should use the following card counting system:
- A = 2
- 2, 3 = 3
- 4 = 1
- 5, 6 = 0
- 7 = -1
- 8, 9 = -2
- T, J, Q, K = -1
I ran two simulations of one hundred million (100,000,000) shoes each using this card counting system, with the cut card placed at its traditional location of 14 cards. In the first simulation, the AP did not shoe-shop, he played every shoe. In the second simulation I assumed the AP did perfect shoe-shopping and only played shoes where the first card was an Ace (only 1 unseen burn card). The following table gives the results of these simulations:
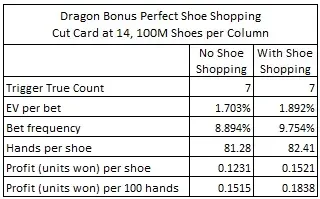
Note that with no shoe-shopping, the AP earns 0.1515 units per 100 hands. With perfect shoe-shopping the AP earns 0.1838 units per 100 hands. This represents a 21.34% increase in the AP's win rate.
In a slow game of baccarat, it takes about 2 hours to play 100 hands. An AP can spend about 17.57% of his time shoe-shopping for Aces and earn about the same as the AP who is playing every shoe. This gives the AP a break-even point of about 10.5 minutes per hour to shop for shoes. If he is using more time than this, on average, then he is losing profitability by shoe-shopping. Any less, then he is gaining profitability. Only 1-in-13 shoes will have an Ace as a first card. This gives the AP about 48 seconds per shoe per hour to find his Ace.
Shoe-shopping only gains value in casino-environments that are packed with baccarat tables. There is no such thing as a Jack Rabbit. For the Dragon Bonus side bet, the time/motion equation may just favor the play-all approach over perfect shoe-shopping.


